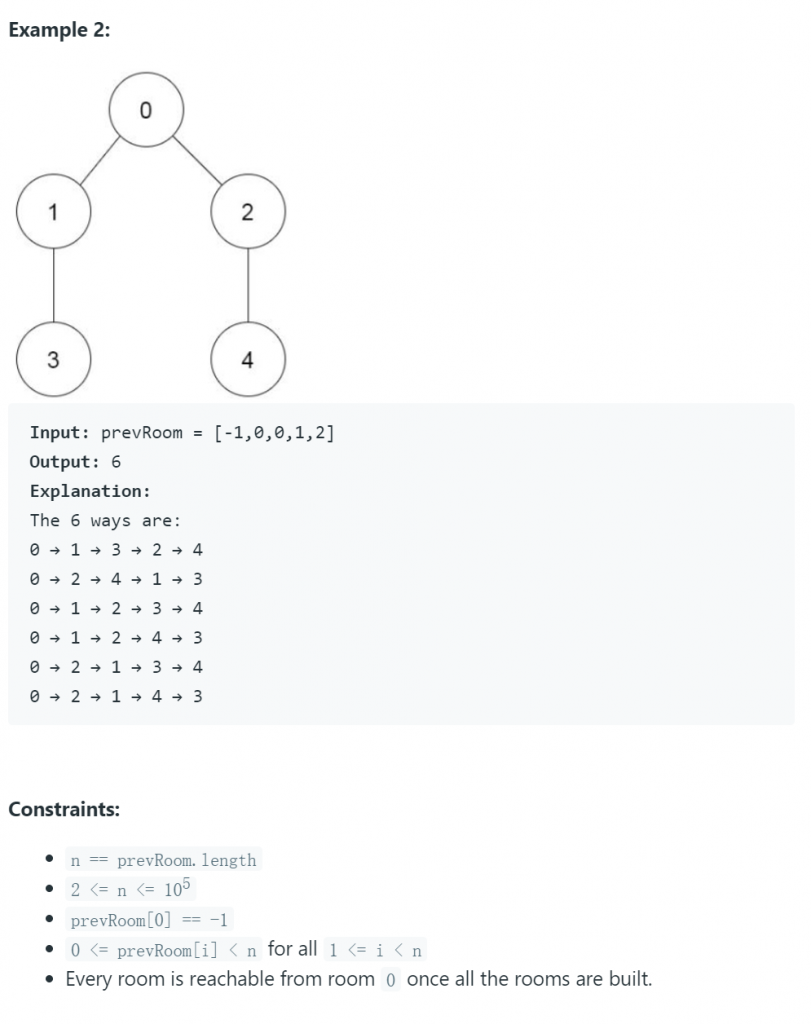
Description

Submission
class Solution {
typedef long long ll;
vector<vector<int>> graph;
vector<ll> dp;
vector<ll> count;
vector<ll> fact;
int n;
const int M = 1e9 + 7;
void dfs(int cur) {
if(graph[cur].empty()) {
dp[cur] = 1;
count[cur] = 1;
return;
}
for(auto x: graph[cur]) {
dfs(x);
}
ll cnt = 0;
for(auto x: graph[cur]) {
cnt += count[x];
}
count[cur] = cnt + 1;
dp[cur] = fact[cnt];
for(auto x: graph[cur]) {
dp[cur] = dp[cur] * dp[x] % M;
}
for(auto x: graph[cur]) {
dp[cur] = dp[cur] * inv(fact[count[x]]) % M;
}
}
ll inv(int x)
{
ll s = 1;
for (; x > 1; x = M%x)
s = s*(M-M/x)%M;
return s;
}
public:
int waysToBuildRooms(vector<int>& prevRoom) {
n = prevRoom.size();
dp.resize(n);
graph.resize(n);
count.resize(n);
fact.resize(n+1);
fact[0] = 1;
for(int i = 1; i <= n; ++i) {
fact[i] = (fact[i-1] * i) % M;
}
for(int i = 1; i < n; ++i) {
graph[prevRoom[i]].push_back(i);
}
dfs(0);
return dp[0];
}
};
// f: factorial
// with n branches
// count = a1 + a2 + a3 + ... + a_n
// f(n) / f(a1) / f(a2) / f(a3) ... f(a_n) * dp[a1] * dp[a2] * dp[a3] ... dp[a_n]



