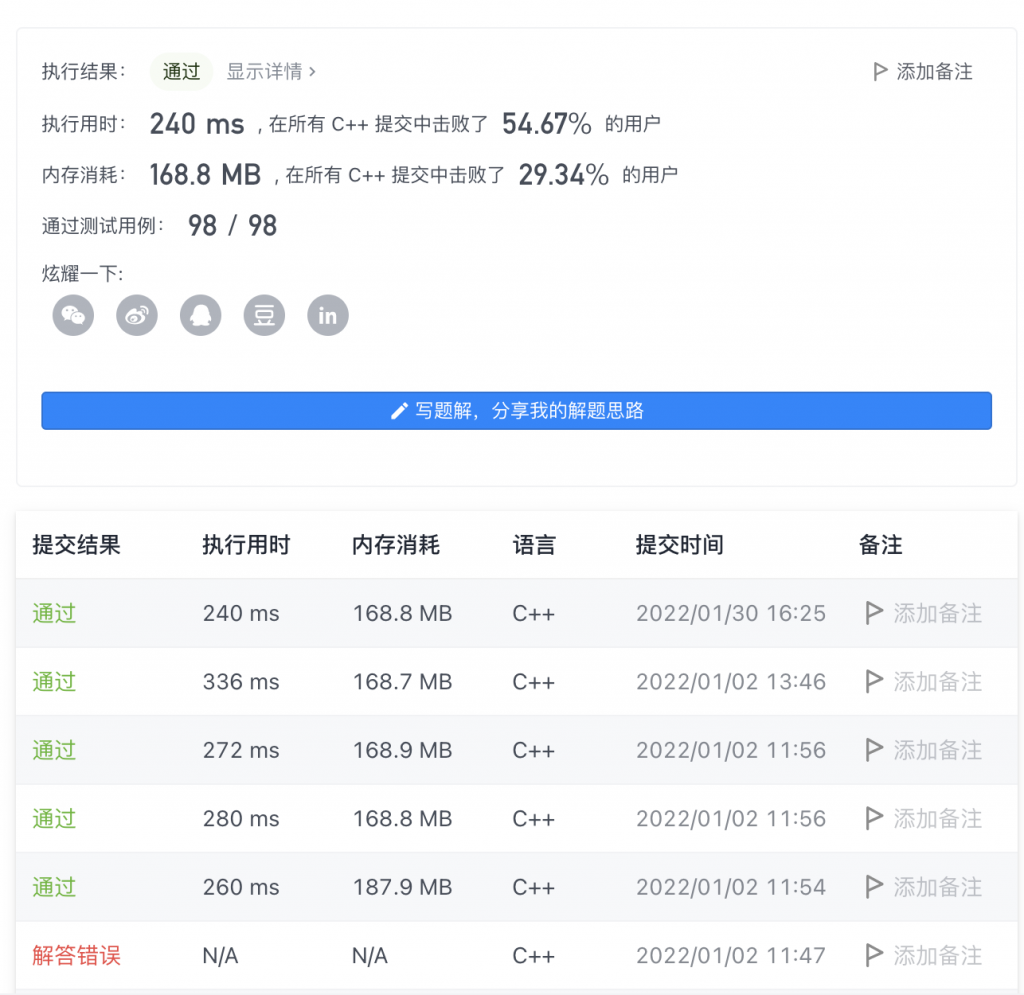
Description

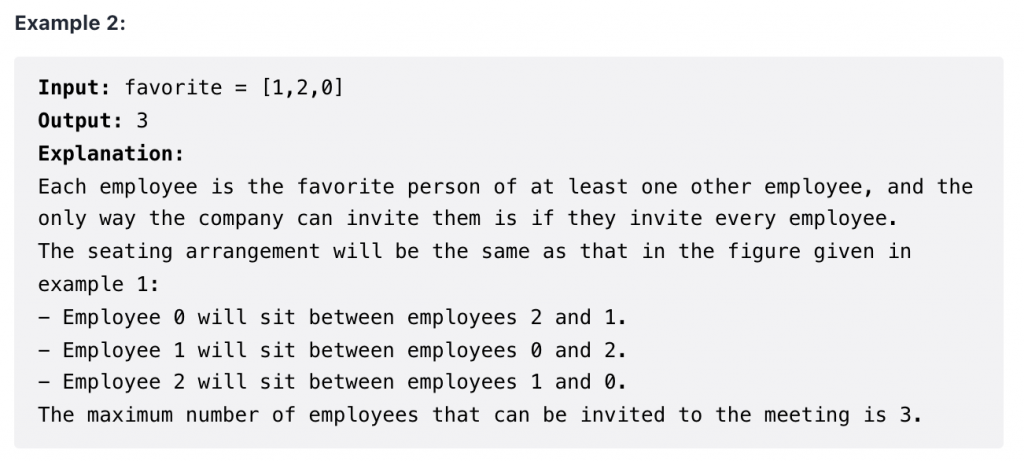
Submission

class Solution {
    vector<int> visited;
    vector<int> visited2;
    vector<int> parent;
    vector<vector<int>> children;
    int cycleEnd = -1;
    int cycleSize = 0;
    int ret;
    int nCycleOfTwo = 0;
    
    void dfs(int cur) {
        if(visited[cur] == 2) return;
        // visiting it the second time, a cycle
        if(visited[cur] == 1) {
            visited[cur] = 2;
            if(cycleEnd == -1) {
                cycleSize = 0;
                cycleEnd = cur;
            }
            return;
        }
        // not visited before
        if(visited[cur] == 0) visited[cur] = 1;
        
        dfs(parent[cur]);
        
        if(cycleEnd != -1) ++cycleSize;
        
        if(visited[cur] == 2) {
            cycleEnd = -1;
            
            if(cycleSize == 2) {
                // take the chain length into account
                fill(visited2.begin(), visited2.end(), 0);
                visited2[parent[cur]] = 1;
                int c1 = dfs2(cur);
                fill(visited2.begin(), visited2.end(), 0); 
                visited2[cur] = 1;
                int c2 = dfs2(parent[cur]);
                nCycleOfTwo += (c1+c2);
            }
            else ret = max(cycleSize, ret);
        }
        
        visited[cur] = 2;
    }
    
    int dfs2(int cur) {
        if(visited2[cur]) return 0;
        visited2[cur] = 1;
        int maxVal = 0;
        for(auto child: children[cur]) {
            maxVal = max(dfs2(child), maxVal);
        }
        return maxVal + 1;
    }
public:
    int maximumInvitations(vector<int>& favorite) {
        ret = 0;
        int n = favorite.size();
        visited.resize(n, 0);
        visited2.resize(n, 0);
        children.resize(n);
        nCycleOfTwo = 0;
        parent = favorite;
        
        for(int i = 0; i < n; ++i) {
            children[parent[i]].push_back(i);
        }
        
        for(int i = 0; i < n; ++i) {
            if(visited[i]) continue;
            
            dfs(i);
        }
        return max(ret, nCycleOfTwo);
    }
};

// 0 1 2 3
// 2 2 1 2
// for cycle size > 2, find the largest cycle
// for cycle size == 2, 2 +  chain length