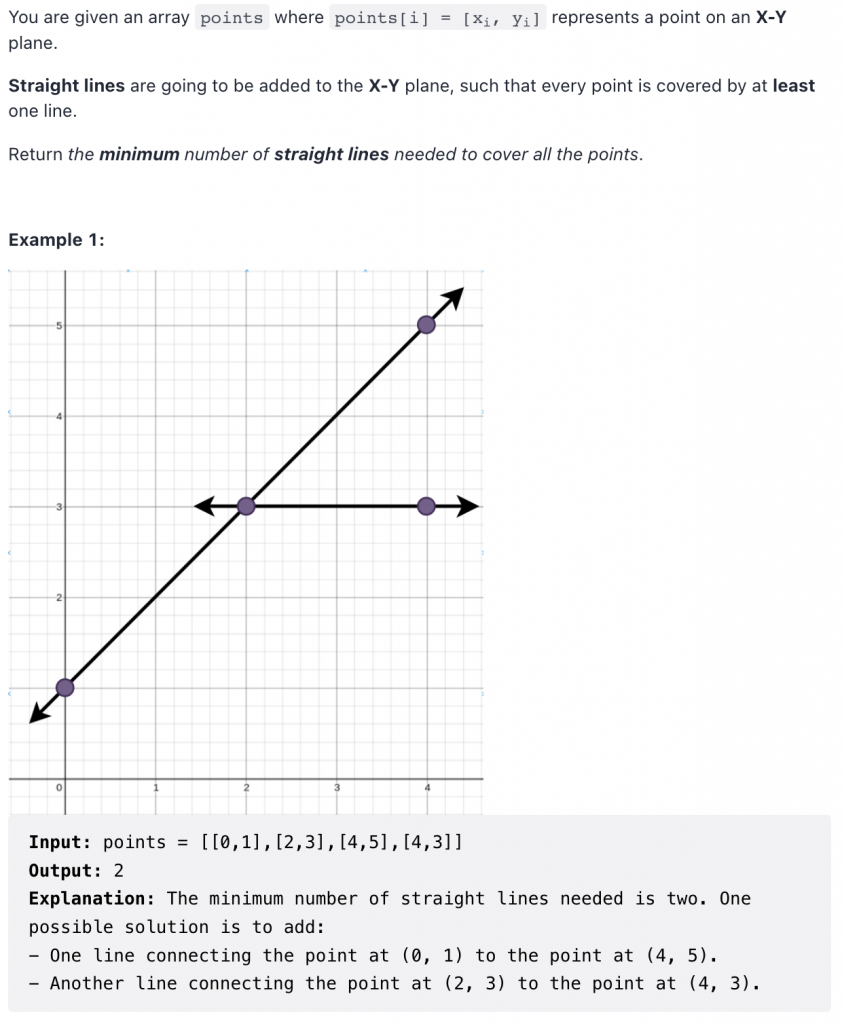
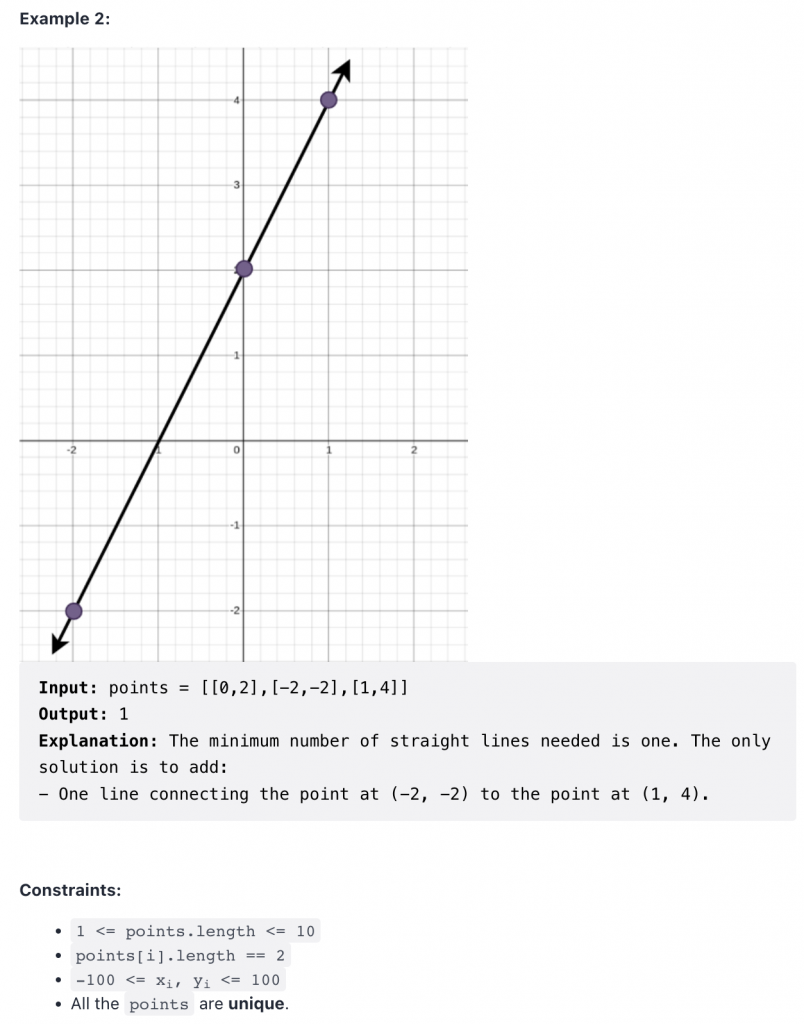
Description

Submission

class Solution {
    int n;
    bool checkInALine(vector<vector<int>>& points, int state) {
        vector<int> v;

        for(int i = 0; i < n; ++i, state >>= 1) {
            if(state&1) v.push_back(i);
        }

        for(int i = 2; i < v.size(); ++i) {
            int a = v[0];
            int b = v[1];
            int c = v[i];

            if((points[a][1] - points[b][1]) * (points[b][0] - points[c][0]) != (points[b][1] - points[c][1]) * (points[a][0] - points[b][0])) return false;
        }

        return true;
    }

    // (y_a - y_b) / (x_a - x_b) = (y_b - y_c) / (x_b - x_c)
public:
    int minimumLines(vector<vector<int>>& points) {
        n = points.size();
        vector<int> dp(1<<n, INT_MAX/2);

        for(int state = 1; state < (1 << n); ++state) {
            int sum = 0;
            if(__builtin_popcount(state) <= 2 || checkInALine(points, state)) {
                dp[state] = 1;
            }
        }


        for(int state = 1; state < (1 << n); ++state) {
            for(int subset = state; subset > 0; subset = (subset-1)&state) {
                dp[state] = min(dp[state], dp[subset] + dp[state-subset]);
            }
        }

        return dp[(1<<n)-1];
    }
};


// dp[state]: the minimum number of lines required to fully cover all the points in state


// k = (y1 - y2) / (x1 - x2)