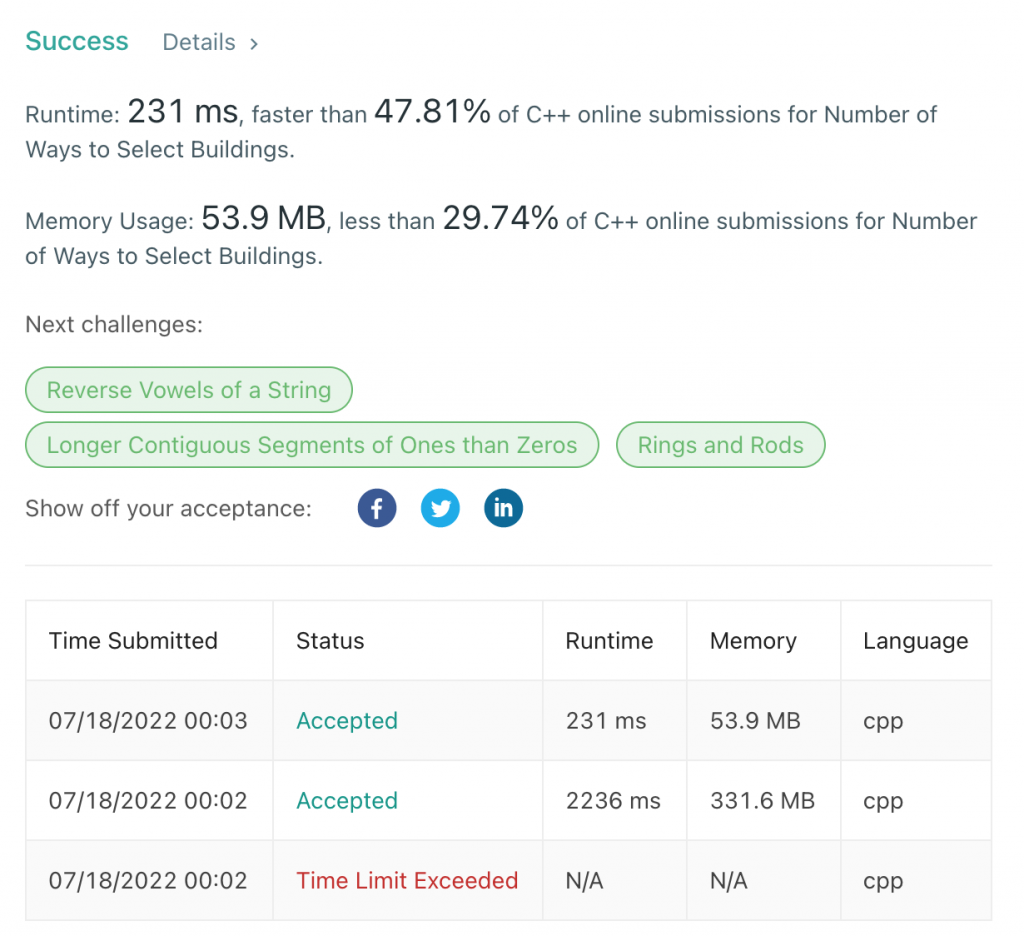
Description

Submission

class Solution {
    using ll = long long;
    ll dp[100005][3][2];
public:
    long long numberOfWays(string s) {
        string t;
        vector<ll> counts;
        for(char ch: s) {
            if(t.empty() || t.back() != ch) {
                t.push_back(ch);
                counts.push_back(1);
            }
            else counts.back()++;
        }

        int n = t.length();
        // vector<vector<vector<ll>>> dp(n, vector<vector<ll>>(3, vector<ll>(2, 0)));
        for(int i = 0; i < n; ++i) {
            ll k = t[i] - '0';
            if(i == 0) {
                dp[i][0][1-k] = 0;
                dp[i][0][k] = counts[i];
                continue;
            }
            for(int j = 0; j < 3; ++j) {
                dp[i][j][1-k] = dp[i-1][j][1-k];
                dp[i][j][k] = dp[i-1][j][k];
                if(j >= 1) dp[i][j][k] += dp[i-1][j-1][1-k] * counts[i];
                else dp[i][j][k] += counts[i];
            }
        }

        return dp[n-1][2][0] + dp[n-1][2][1];

    }
};

// dp[i][j][k]: number of ways ending with i-index(whether taken or not), selected j numbers so far, the subsequence ends with k


// for(int j = 0; j < 3; ++j) {
//     if(s[i] == '0') {
//         dp[i][j][1] = dp[i-1][j][1];
//         dp[i][j][0] = dp[i-1][j-1][1] + dp[i-1][j][0];
//     } else {
//         dp[i][j][0] = dp[i-1][j][0];
//         dp[i][j][1] = dp[i-1][j-1][0] + dp[i-1][j][1];
//     }
// }