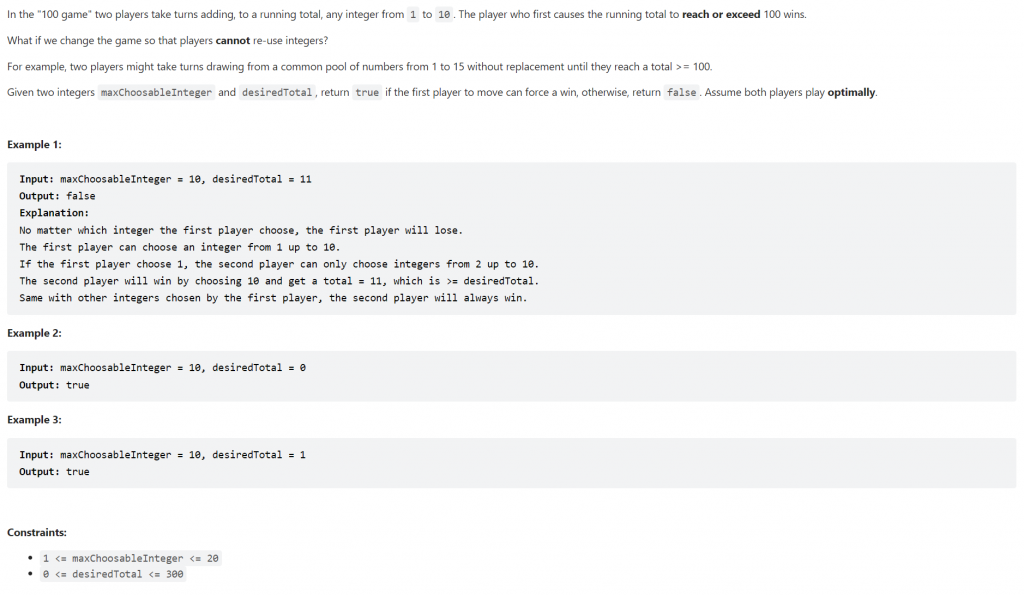
Description

Submission

class Solution {
    int visited[1<<21];
public:
    bool canIWin(int maxChoosableInteger, int desiredTotal) {
        int totalSum = (1 + maxChoosableInteger) * maxChoosableInteger / 2;
        if(totalSum < desiredTotal) return false;
        return dfs(0, 0, maxChoosableInteger, desiredTotal);
    }

    bool dfs(int state, int sum, int maxChoosableInteger, int desiredTotal) {
        if(visited[state]) return visited[state] - 1;
        
        for(int i = 1; i <= maxChoosableInteger; ++i) {
            if((state>>i)&1) continue;

            if(sum + i >= desiredTotal) {
                visited[state] = 2;
                return true;
            }

            // if the other player cannot win, choose this strategy
            if(dfs(state + (1<<i), sum + i, maxChoosableInteger, desiredTotal) == false) {
                visited[state] = 2;
                return true;
            }
        }

        visited[state] = 1;
        return false;
    }
};