These are the notes I took when learning Week 1 & 2 of the course Machine Learning with Python at Coursera.
AI, Machine Learning, Deep Learning
- ML is the statistics part of AI
- Deep Learning is a special part of ML
Major machine learning techniques
- Regression / Estimation: Predicting continuous values
- Classsification: Predicting the item clas / catefory of a case
- Clustering: finding the structure of data; summarization
- Associations: Associating frequent co-occurring itmes/events
- Anomaly detection: discovering abnormal and unusual cases
- Sequence minging: predicting next events; click-stream(Markov Model, HMM)
- Dimension Reduction: Reducing the size of data(PCA)
- Recommendation systems: Recommneding items
Python Libraries
- Numpy
- Scipy
- matplotlib
- pandas
- scikit learn
Supervised vs Unsupervised
Supervised Learning
Deals with labeled data
- regression
- classification
Unsupervised learning
finds patterns and groupings from unlabeled data
Techniques
- Dimension Reduction
- Density Estimation
- Market basket analysis
- clustering
- Discovering structure
- summarization
- Anomaly detection
Regression
the process of predicting a continous value
- X: Independent variable
- Y: Dependent variable, continuous
Regression can be
- linear
- non-linear
Simple Regression
One feature to predict anohter
Multiple Regression
Many feactures to predict one
Linear Regression
Signle Linear Regression
: response variable, predicted value
: a single predictor
: intersect
: slope, gradient, coefficient
Residual value: the error,
Calculation of 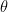 ‘s
‘s

Multiple Linear Regression
Estimate 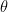
- Ordinary Least Squares
- Linear algebra operations
- Takes a long time for large datasets(10K+ rows)
- An optimization algorithm
- Gradient Descent
- Stochastic Gradient Descent
- Newton’s Method
OLS: Ordinary Least Squares
Should firstly use scatter plot to visualize if the plot is linear
Polynomial Regression
Polynomial Regression Multiple Linear Regression
Least Squares
- Least Squares: Minimizing the sum of the squares of the differences between
and
Non-linear Regression
Examples
Quadratic

Expnential

Logarithmic

Sigmoidal/Logistic

Fit Process
Plotting the Dataset

Choosing a model
The Sigmoidal might fit.

: Controls the curve’s steepness
: Slides the curve on the x-axis
Building the Model
Contruct the model function
def sigmoid(x, Beta_1, Beta_2):
y = 1 / (1 + np.exp(-Beta_1*(x-Beta_2))
return y
Visualize and Compare with an initial value
beta_1 = 0.10
beta_2 = 1990.0
# logistic function
Y_pred = sigmoid(x_data, beta_1, beta_2)
# plot initial prediction against datapoirnts)
plt.plot(x_data, Y_pred*15000000000000.)
plt.plot(x_data, y_data, 'ro')

Then normalize x and y before finding the parameters
xdata = x_data / max(x_data)
ydata = y_data / max(y_data)
curve_fit uses non-linear least squares to fit our sigmoid function
from scipy.optimize import curve_fit
popt, pcov = curve_fit(sigmoid, xdata, ydata)
# print the final parameters
print(" bata_1 = %f, bata_2 = %f" % (popt[0], popt[1]))
Then plot to see if that model works well
x = np.linspace(1960, 2015, 55)
x = x/max(x)
plt.figure(figsize=(8,5))
y = sigmoid(x, *popt)
plt.plot(xdata, ydata, 'ro', label='data')
plt.plot(x,y, linewidth=3.0, label='fit')
plt.legend(loc='best')
plt.ylabel('GDP')
plt.xlabel('Year')
plt.show()

Evaluation
We can verify the accuracy of our model by using model evaluation.
# write your code here
from sklearn.metrics import r2_score
# split data into train/test
msk = np.random.rand(len(df)) < 0.8
train_x = xdata[msk]
test_x = xdata[~msk]
train_y = ydata[msk]
test_y = ydata[~msk]
# build the model using train set
popt, pcov = curve_fit(sigmoid, train_x, train_y)
# predit using the test set
y_hat = sigmoid(test_x, *popt)
print("Mean absolute error: %.4f" % np.mean(np.absolute(y_hat - test_y)))
print("Residual sum of squares (MSE): %.6f" % np.mean((y_hat - test_y) ** 2))
print("R2-score: %.2f" % r2_score(y_hat , test_y) )

Model evaluation approaches

Training and Test on the Same Dataset

- High training accuracy
- Low out-of-sample accuracy
Training Accuracy
- High Accuracy is not always good: outfit, capture noise and produce a non-generalized model

Out-of-Sample Accuracy
The accuracy of predicting unkown dataset
Train/Test Split
- mutually exclusive
- More accurate evaluation on out-of-sample accuracy
- highly
K-fold cross-validation
Split the data into k-folds, and each fold as a testing data set and the rest and rest as training set to train the model. The overall accuracy is the average of the k-folds.

Regression Evaluation Metrics
- MAE: mean absolute error
- MSE: mean squared error
- RMSE: root mean squared error
- RAE: Relative Absolute Error
- RAE: Relative Squared Error